Comp 150 Notes on counting strings and other things
Updated 1 February 2017. Recent updates are in red.
There is a traditional English
nursery rhyme that is also a riddle. It dates from about
1730.
As I was going to St. Ives,
I met a man with seven wives,
Each wife had seven sacks,
Each sack had seven cats,
Each cat had seven kits:
Kits, cats, sacks, and wives,
How many were there going to St. Ives?
The answer to the riddle may be in
dispute (see the Wikipedia article),
but the total number of kits, cats, sacks, and wives --
wherever they might be going -- shouldn't
be. (But even the hokey answer can
come in handy, sometimes.)
The computation is part of a vast
area of mathematics called combinatorics: the
science of counting things in their various groupings,
orderings, and combinations. Combinatorics is
essential to the study of computational complexity,
which deals with the problem of working out ahead of
time how long a program is going to take before
producing an answer and coming to a halt. Basic
computational tasks such as searching and sorting, as
simple as they might sound, are tremendously important
in the modern day -- for example, searching and sorting
is largely what Google Search spends all day
doing. Just a few minutes ago (as I wrote this) I
searched for the phrase "As I was going to St. Ives",
and Google instantly responded with the information that
throughout the entire internet (five billion web pages),
there are 36,000 web pages relevant to my search. Google
had already found and sorted them in order of importance
or relevance, and led with the top of the list (the
Wikipedia article). And all this in less than half a
second. To be lightning fast on such an imposing task
takes careful planning, and a lot of work. There are
many, many algorithms for searching and sorting, and
they all have their sweet and their bitter spots in
terms of where they work well, compared to other
algorithms. Combinatorics has a big role in determining
which algorithms to use, in which cases.
Combinatorics, with number theory, also provides the
foundation of cryptography and online security.
In this course, we won't be going
any further than a mere toe-dip into the vast sea of
combinatorics, but we will dip that toe. And the little
knowledge obtained will be sufficient to enable you to
calculate how long it takes to find (say) all
five-letter words, or to find all anagrams of a given
word or phrase. If you're interested in learning more,
combinatorics appears in detail in Math 318 and 418, and
Comp 163 and 363. The most comprehensive treatment of
the topic is a multi-volume work called The Art of
Computer Science, by Donald Knuth, whose official
title at Stanford University is Professor of the Art of
Computer Science.
• •
Check out this thirty-second video
in which Dweezil
Zappa introduces combinatorics < broken link (Square One
TV, Episode 110, 1987), as well as this Vimeo video by
thatoliverguy called The Fundamental
Counting Principle in Use.
We'll do a slightly different
example, and explain why the Fundamental Counting
Principle is true along the way.
The set-up: you want to buy a
T-shirt from an online provider. There are four choices
of a logo to be printed on the shirt (we'll abstract
these images by using the numbers 1, 2, 3, 4) and there
are three choices of color (red, green, and blue).
How many different T-shirts are available? As we go
about answering that question, we'll also come up with a
methodical technique (an algorithm) for listing
all the combinations.
One way to think of the totality of
the possibilities is by considering the groups that they
naturally fall into. There are four different logos, so
the T-shirts can be grouped by logo: Group 1, Group 2,
Group 3, and Group 4. Each of these groups has
T-shirts with that particular logo, but in three
different colors. There are thus four groups of three
T-shirts each. Four logos, each three times.
Four times three. 4 × 3. And you know from
memory that 4 × 3 = 12. This is the most basic
conceptual definition of multiplication: when you have m
groups of n items, there are m × n
items altogether.
Fundamental Counting Principle
If you have m boxes of n items, then the
total number of items is given by m × n.
(I'll note in passing that the algorithm you learned in
elementary school for multiplying integers in base-ten
is not the "definition" of multiplication.
Multiplication was understood millennia before people
learned how to multiply digit by digit in base-10, with
carrying and adding a column of numbers. This method of
multiplication was invented by the Indian mathematician
and astronomer Brahmagupta
in the seventh century. This algorithm was actually unknown
to European mathematicians for another thousand years.)
A useful way to look at the number
of combinations of logos and colors, and to see how to
list them methodically, is with a graph.
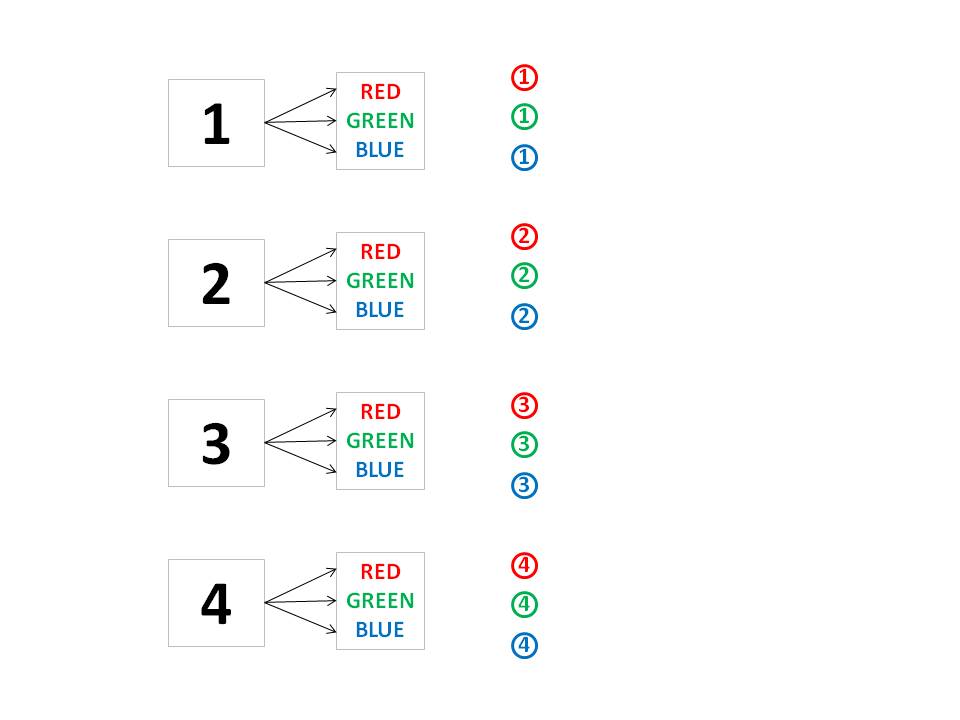
In the first column, we
have the logo possibilities (four of them), and in the
second column we have, for each of the four possible
logos, the color possibilities (three of them), for a
total of four groups of three T-shirts. In the last
column, we see the actual combinations of logo and color
by reading the graph from top to bottom. So, not
only can you see that there are 4 × 3 = 12
possibilities, but you can also list the possibilities
methodically. This latter might not seem a big deal, but
without such a method, and with a larger number of
choices, it could be easy to miss one of the
combinations. This is even more evident when you
consider more options than just two (here logo and
color).
Now let's consider the case where there is an additional option. For the given logos, one can choose either a round border or a square border. You might be reasoning already that we had 12 possibilities for T-shirts and colors before, and now, for each of those possibilities, there are 2 different options to choose from, so that there are 12 × 2 = 24 possibilities. And this would be correct.
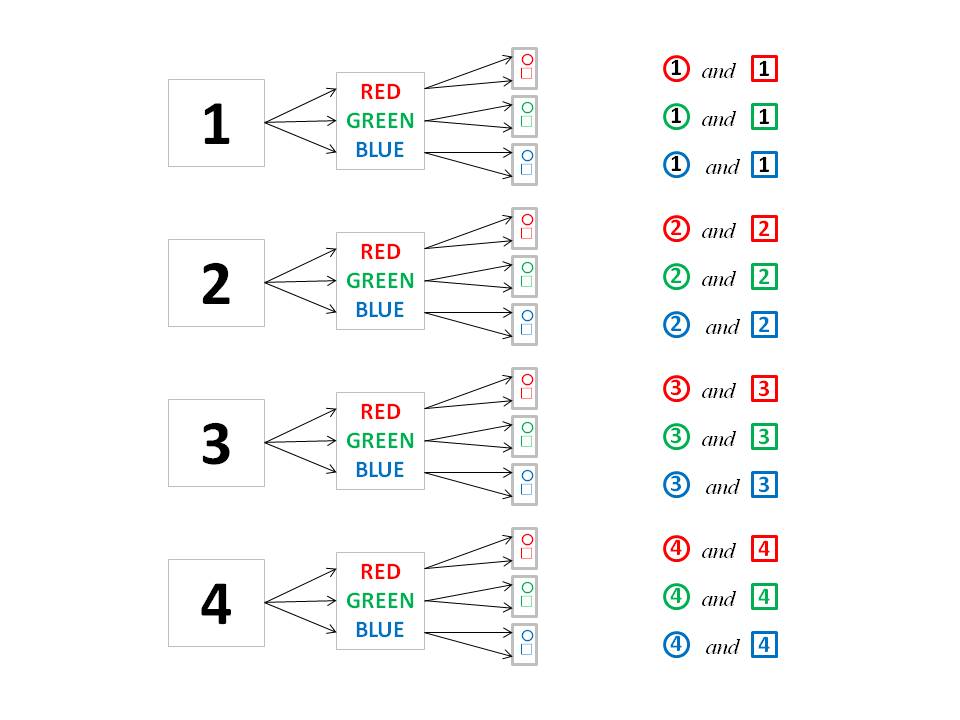
In general, if you have m boxes, and each of those boxes contains p smaller boxes, and each of those smaller boxes contain q items, then the total number of items is m × p × q. This seems like a more general version of the Fundamental Counting Principle, but it's really just two applications of the old principal, as stated above.
And, not only that, but once you've constructed the graph, it's easy to write down all the combinations. There they are, in the last column. The combinations are found by following all directed paths from left to right in the graph. Graphs like this are used extensively in computer science.
Exercise. Watch the short video The Fundamental Counting Principle in Use and draw a graph, like the one above, to show all the possible outfits.
The Fundamental Counting Principle extends to any number of options, not just two or three, as long as the choices are independent of each other. (An example of a dependency might be: "Logo 2 only comes in red." or "Square logos are not available in blue.") This further elaboration of the principle can be written mathematically as
The Fundamental Counting Principle
If there are n different options, numbered 1, 2, 3, . . . , k, . . . , n, and if for each option k between 1 and n there are ck possibilities for option k, then the total number of possibilities is given by c1 × c2 × c3 × . . . × c n.
The number of strings of length n from a character set of size c.
Now we can give a more satisfying answer to the question of how many strings there are of length n from a character set of size c. For our first example, let's consider a very limited character set of just three characters: A, B, and C. The strings of length 1 are just A, B, and C themselves: there are three of them. The strings of length two are easy to list, but for practice, let's make a graph, as we did above for the colored shirts with square or round logos.
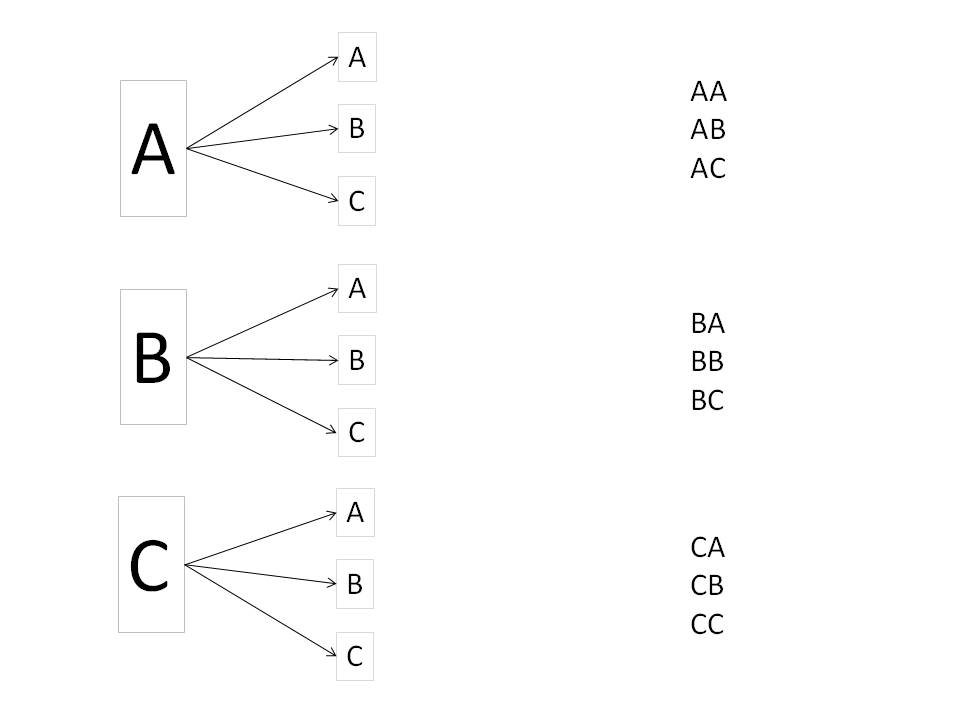
Let's continue and consider three-letter strings. This case starts out just like the case for two-letter strings, but further, for each two-letter string there are three possibilities for the third character.
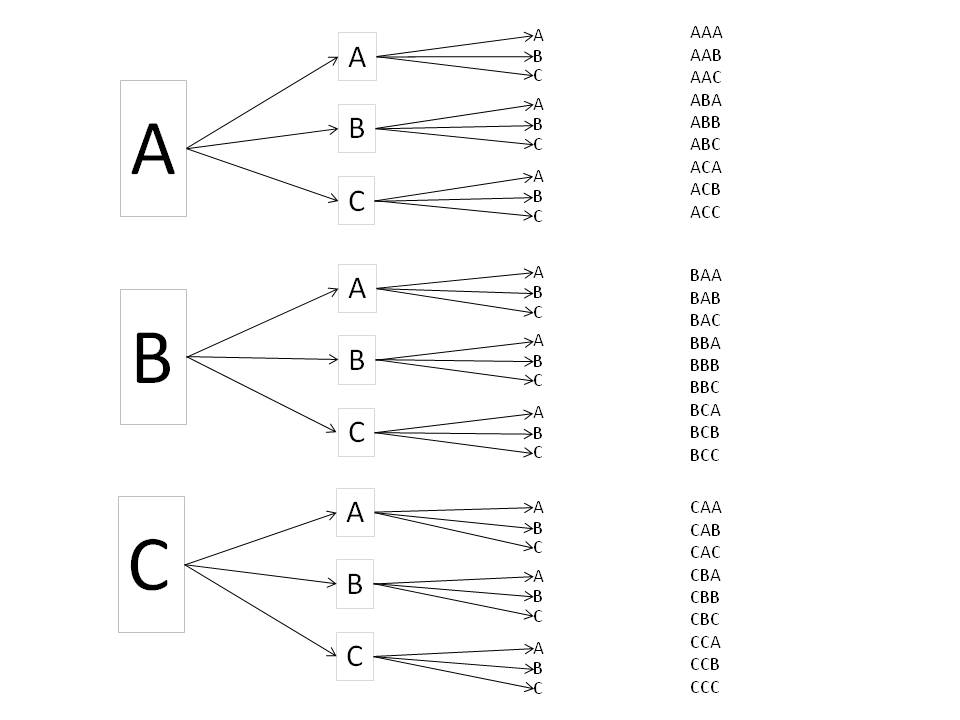
When it comes to larger character sets and string lengths, it becomes more difficult to draw these graphs with pencil on paper (or even with powerpoint, which is what I used to make the images in these notes). In your later courses, should you pursue them, you'll find that the way to handle very large graphs is by constructing them with a computer program -- not to be printed out, but to be manipulated abstractly. But still, for the kind of number-of-strings problem we're considering here, there are is a practical way of handling the computations by applying the Fundamental Counting Principle directly.
For our next example, let's take the character set to be the twenty-six capital letters of the Latin alphabet: A, B, C, . . . , Z. So c = 26.
Let's first consider strings in this character set of length two, so that n = 2. Think of a character string of length two as two squares in a row, each square representing the location of a character in the string.
In the first square, you can put in any letter you want-- there are 26 choices. And for the second square, there are again 26 choices. So by the Fundamental Counting Principle, there are 26 × 26 strings of length two.
(One way to think of this with boxes (as in shoe boxes) -- and this may take a little bit of creative cogitation, --is like this: For each letter of the character set there is a box labeled with that character. And each of those boxes contains 26 smaller boxes, each of them labeled with the letters of the character set. The total number of little boxes, which by dint of its location in a labeled box represents a two-character string, is 26 × 26.)
Now let's consider strings of length three, so that n = 3. Think of a character string of length three as three squares in a row, one square for each character:
There are two ways, using the Fundamental Counting Principle, of thinking about how many possibilities there are. First, you already know that there are 26 × 26 ways to fill in the first two boxes. And for each one of these way, there are 26 ways to fill in the third box, making a total of (26 × 26) × 26. A second way is simply to use the Fundamental Counting Principle for multiple independent choices that we have already discussed and simply multiply all the possibilities together: 26 × 26 × 26. It's the same value in either case, of course.
(If you want to think of this in terms of shoe boxes: there are 26 boxes, each labeled with a letter from A to Z. Within each of these boxes, there are 26 smaller boxes, each of them labeled with a letter from A to Z. And within each of those boxes there are 26 still smaller boxes, each of them labeled with a letter from A to Z. So there are26 × 26 × 26 of the smallest boxes, and each one of them represents a string of length three. Its label represents the third character of the string, the label of the box it's in represents the second letter, and the label of the box containing that box represents the first letter.)
Now let's consider strings of length four, so that n = 4.
By the Fundamental Counting Principle, there are 26 possibilities for each of 4 options (the squares), and so the total number of possibilities is 26 × 26 × 26 × 26.
A pattern should be emerging in your mind. If one were to consider strings of length 12 (from this character set),
then the total number of possibilities is 26 × 26 × 26 × 26 × 26 × 26 × 26 × 26 ×26 × 26 × 26 × 26. This figure is written more compactly as 2612. But the best way to think of this, so that you don't get confused, is as a long product, as long as the length of the string.
In general, if you want to compute the number of strings of length n from a character set of size c, the total number is c × c × c × . . . × c, where there are n factors of c listed. In other words, we have the following.
String-counting formula.
The number of strings of length n from a character set of size c is c n.
- The license plate codes must be
three characters long.
- The first character must be a
circle, a square, a triangle, or a star.
- The second character must be a 0 or a 1.
- The third character must be an A, a B, or a C.
Exercise. Suppose a security code (or PIN) can be any string of five digits, including zeros. How many security codes are there?
Exercise. Suppose a security code can be any string of five or fewer digits in length. How many security codes are there?
Exercise. How many were going to St. Ives? Justify your answer.
Exercise. A typical
image on the internet is of size 640 × 480. (How
many pixels does it contain?) Let's focus on
images of a smaller size, say 10 × 10 (about the size of
an alphabetic character on the screen). And
let's assume there are just two possible colors for each
pixel, black and white. How many different possible
black-and-white 10 × 10 images are there? Use the python
shell to compute this number. How many digits
does it have?
Exercise. The colors on
your computer screen are specified using what is called
the RGB Color Model. In this model, red, green,
and blue colored light are combined in a given pixel to
create a color for that pixel. Each of the colors
red, green, and blue have 256 different possible
shades. How many possible colors are there for a
given pixel? (You may use the Idle shell to
compute this.)
Here are some
interesting (and optional) references about color: The
RGB Color Model (Wikipedia), Can
my computer really display millions of colors?,
An
RGB Image Showing All Possible Colors.
Exercise. Now let's get
back to the standard image of size 640 × 480. How many
pixels does it contain? If each pixel can be a different
color in the RGB model, how many different possible
color pictures of this size are there? For this
problem, you can just write a mathematical or a python
expression for the answer; you don't have to compute it.
Exercise. An anagram
for a word or phrase is another word or phrase that
uses all the same letters, the same number of times.
(For phrases, you can change the number of spaces,
the punctuation, and the capitalization, but the
letters have to stay the same.) For example, "post"
and "stop" are anagrams. The phrases "Clint Eastwood"
and "Old West action!" are anagrams. One of my
favorites pairs of anagrams, which might be due to
Martin Gardner, is "eleven plus two" and "twelve plus
one". (a) Consider the word "post". I want you to
compute the number of different possible
anagrams of "post", ignoring for the moment whether
they are actual English words or not. (b) Use a
graph to figure out the list of all possible anagrams
of "post". (c) Which of these strings are actual
English words? (d) Go to the Internet
Anagram Server and see if you can find an
interesting anagram of your name. How do you
suppose the Anagram Server works?
Copyright © 2016 Curtis Tuckey. All rights reserved. ctuckey@luc.edu